| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 6 (Before Exercise 8.1) | Exercise 8.1 | Example 7 & 8 (Before Exercise 8.2) |
| Exercise 8.2 | ||
Chapter 8 Quadrilaterals
Welcome to this detailed guide covering the solutions for Chapter 8: Quadrilaterals. This chapter significantly advances our geometric understanding by shifting focus from three-sided figures to the diverse world of four-sided polygons. Building upon concepts likely introduced in Class 8, this exploration demands a greater level of rigor, particularly in constructing formal proofs related to the properties and classifications of various quadrilaterals. We will delve into the fundamental characteristics that define these shapes, with a special emphasis on the critically important category of parallelograms and their unique derivatives.
Our journey begins by reaffirming the foundational angle sum property of a quadrilateral, stating that the sum of the interior angles of any four-sided figure invariably equals $360^{\circ}$. However, the core of the chapter, and consequently these solutions, revolves around the extensive study of parallelograms. A parallelogram is a quadrilateral with specific defining features, leading to a rich set of derived properties. The provided solutions meticulously detail the proofs for these essential characteristics, often relying on triangle congruence established in the previous chapter:
- Proof that a diagonal divides a parallelogram into two congruent triangles.
- Demonstration that opposite sides of a parallelogram are always equal in length.
- Proof showing that opposite angles within a parallelogram are equal.
- Establishing that the diagonals of a parallelogram bisect each other (meaning they intersect at their midpoints).
Conversely, it's equally important to know the conditions under which an arbitrary quadrilateral can be definitively classified as a parallelogram. The solutions provide clear, step-by-step proofs for these sufficient conditions:
- If both pairs of opposite sides of a quadrilateral are equal, then it is a parallelogram.
- If both pairs of opposite angles are equal, then it is a parallelogram.
- If the diagonals of a quadrilateral bisect each other, it must be a parallelogram.
- Crucially, if just one pair of opposite sides is proven to be both equal and parallel, this is sufficient to confirm the quadrilateral is a parallelogram.
These properties and conditions are not merely theoretical; the solutions guide students in applying them practically to solve numerical problems (e.g., finding unknown angles or side lengths) and to structure proofs demonstrating that a specific geometric figure is indeed a parallelogram. Furthermore, the chapter revisits special types of parallelograms – namely rectangles, rhombuses, and squares – exploring their unique additional properties (like equal diagonals in a rectangle, or perpendicular diagonals in a rhombus) which are often proven using the foundational parallelogram theorems combined with triangle congruence.
A highlight of this chapter is the introduction and application of the highly significant Mid-point Theorem. This theorem states that the line segment connecting the mid-points of any two sides of a triangle is necessarily parallel to the third side and, importantly, is equal to half the length of the third side (length = $\frac{1}{2} \times \text{length of third side}$). The solutions present the proof, frequently involving auxiliary constructions and leveraging parallelogram properties, and demonstrate its utility in various problems. The converse of the Mid-point Theorem is also covered, stating that a line drawn through the mid-point of one side of a triangle, parallel to another side, will bisect the third side. Emphasis throughout these solutions is placed squarely on deductive reasoning, the logical construction of proofs, and the accurate application of theorems in diverse geometric scenarios.
Example 1 to 6 (Before Exercise 8.1)
Example 1. Show that each angle of a rectangle is a right angle.
Answer:
Given:
ABCD is a rectangle.
To Prove:
Each angle of rectangle ABCD is a right angle, i.e., $\angle A = \angle B = \angle C = \angle D = 90^\circ$.
Proof:
By definition, a rectangle is a parallelogram in which one angle is a right angle.
Let ABCD be a rectangle.
Since ABCD is a parallelogram, we know that opposite sides are parallel.
So, AB $||$ DC and AD $||$ BC.
Let's assume $\angle A = 90^\circ$ (by definition of rectangle).
Since AD $||$ BC and AB is a transversal, the sum of consecutive interior angles is $180^\circ$.
$\angle A + \angle B = 180^\circ$
(Consecutive interior angles)
Substituting $\angle A = 90^\circ$:
$90^\circ + \angle B = 180^\circ$
$\angle B = 180^\circ - 90^\circ$
$\angle B = 90^\circ$
Also, in a parallelogram, opposite angles are equal.
$\angle C = \angle A$
(Opposite angles of parallelogram)
$\angle C = 90^\circ$
$\angle D = \angle B$
(Opposite angles of parallelogram)
$\angle D = 90^\circ$
Thus, all angles of the rectangle ABCD are $90^\circ$.
Hence, each angle of a rectangle is a right angle.
Example 2. Show that the diagonals of a rhombus are perpendicular to each other.
Answer:
Given:
ABCD is a rhombus.
Diagonals AC and BD intersect at point O.
To Prove:
The diagonals AC and BD are perpendicular to each other, i.e., $\angle AOB = \angle BOC = \angle COD = \angle DOA = 90^\circ$.
Proof:
Since ABCD is a rhombus, it is also a parallelogram.
In a parallelogram, diagonals bisect each other.
OA = OC
(Diagonals of parallelogram bisect each other)
OB = OD
(Diagonals of parallelogram bisect each other)
Also, in a rhombus, all sides are equal.
AB = BC = CD = DA
(Sides of a rhombus)
Now, consider $\triangle AOD$ and $\triangle COD$.
OA = OC
(Proved above)
OD = OD
(Common side)
AD = CD
(Sides of a rhombus)
Therefore, by SSS congruence rule:
$\triangle AOD \cong \triangle COD$
By Corresponding Parts of Congruent Triangles (CPCT):
$\angle AOD = \angle COD$
... (i)
Since AC is a straight line segment, BD stands on it.
Therefore, $\angle AOD$ and $\angle COD$ form a linear pair.
$\angle AOD + \angle COD = 180^\circ$
(Linear pair axiom)
From (i):
$\angle AOD + \angle AOD = 180^\circ$
$2 \angle AOD = 180^\circ$
$\angle AOD = \frac{180^\circ}{2}$
$\angle AOD = 90^\circ$
So, $\angle COD = \angle AOD = 90^\circ$.
Similarly, $\angle AOB = \angle BOC = 90^\circ$.
Thus, the diagonals AC and BD are perpendicular to each other.
Example 3. ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD || AB (see Fig. 8.14). Show that
(i) ∠DAC = ∠BCA and
(ii) ABCD is a parallelogram.
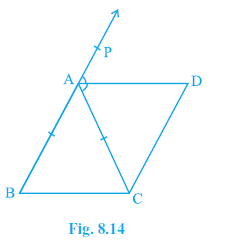
Answer:
Given:
$\triangle ABC$ is an isosceles triangle with AB = AC.
AD bisects the exterior angle PAC.
CD $||$ AB.
To Prove:
(i) $\angle DAC = \angle BCA$
(ii) ABCD is a parallelogram.
Proof:
Part (i): $\angle DAC = \angle BCA$
In $\triangle ABC$, AB = AC (Given).
Therefore, angles opposite to equal sides are equal.
$\angle ABC = \angle BCA$
[Angles opposite equal sides] ... (1)
The exterior angle PAC is equal to the sum of the two opposite interior angles.
$\angle PAC = \angle ABC + \angle BCA$
[Exterior angle theorem]
Using (1):
$\angle PAC = \angle BCA + \angle BCA$
$\angle PAC = 2 \angle BCA$
... (2)
AD bisects $\angle PAC$ (Given).
Therefore,
$\angle PAC = 2 \angle DAC$
... (3)
From (2) and (3):
$2 \angle DAC = 2 \angle BCA$
$\angle DAC = \angle BCA$
Hence, part (i) is proved.
Part (ii): ABCD is a parallelogram
We have just proved $\angle DAC = \angle BCA$.
These are alternate interior angles for lines AD and BC intersected by transversal AC.
Since the alternate interior angles are equal, the lines AD and BC must be parallel.
AD $||$ BC
Also, it is given that:
CD $||$ AB
Since both pairs of opposite sides of quadrilateral ABCD are parallel (AD $||$ BC and AB $||$ CD), ABCD is a parallelogram.
Hence, part (ii) is proved.
Example 4. Two parallel lines l and m are intersected by a transversal p (see Fig. 8.15). Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
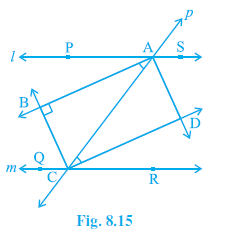
Answer:
Given:
Line $l \parallel m$.
Transversal $p$ intersects $l$ at A and $m$ at C.
The bisectors of interior angles $\angle PAC$, $\angle ACQ$, $\angle ACR$, and $\angle SAC$ form a quadrilateral ABCD.
(Let the intersection points of bisectors be B and D as shown in standard figures, or name the angles properly based on the provided figure. Assuming the points are such that AB bisects $\angle PAC$, CB bisects $\angle ACQ$, CD bisects $\angle ACR$, AD bisects $\angle SAC$).
So, AB, BC, CD, DA are the bisectors of $\angle PAC$, $\angle ACQ$, $\angle SAC$, $\angle ACR$ respectively.
To Prove:
The quadrilateral ABCD formed by the bisectors is a rectangle.
Proof:
Since $l \parallel m$ and $p$ is a transversal, the sum of interior angles on the same side of the transversal is $180^\circ$.
$\angle PAC + \angle ACR = 180^\circ$
(Consecutive Interior Angles)
AD bisects $\angle PAC$ and CD bisects $\angle ACR$.
$\angle DAC = \frac{1}{2} \angle PAC$
$\angle ACD = \frac{1}{2} \angle ACR$
Therefore,
$\frac{1}{2} \angle PAC + \frac{1}{2} \angle ACR = \frac{1}{2} \times 180^\circ$
$\angle DAC + \angle ACD = 90^\circ$
... (1)
In $\triangle ADC$, the sum of angles is $180^\circ$.
$\angle DAC + \angle ACD + \angle ADC = 180^\circ$
(Angle sum property of triangle)
Using (1):
$90^\circ + \angle ADC = 180^\circ$
$\angle ADC = 180^\circ - 90^\circ = 90^\circ$
Similarly, considering the interior angles $\angle SAC$ and $\angle ACQ$:
$\angle SAC + \angle ACQ = 180^\circ$
(Consecutive Interior Angles)
AB bisects $\angle SAC$ and CB bisects $\angle ACQ$.
$\frac{1}{2} \angle SAC + \frac{1}{2} \angle ACQ = \frac{1}{2} \times 180^\circ$
$\angle BAC + \angle ACB = 90^\circ$
... (2)
In $\triangle ABC$, the sum of angles is $180^\circ$.
$\angle BAC + \angle ACB + \angle ABC = 180^\circ$
(Angle sum property of triangle)
Using (2):
$90^\circ + \angle ABC = 180^\circ$
$\angle ABC = 180^\circ - 90^\circ = 90^\circ$
Now, consider the angles $\angle PAC$ and $\angle ACQ$. They form a linear pair.
$\angle PAC + \angle SAC = 180^\circ$
(Linear Pair)
Dividing by 2:
$\frac{1}{2}\angle PAC + \frac{1}{2}\angle SAC = 90^\circ$
$\angle DAC + \angle BAC = 90^\circ$
So, $\angle DAB = 90^\circ$.
Similarly, consider $\angle ACR$ and $\angle ACQ$. They form a linear pair.
$\angle ACR + \angle ACQ = 180^\circ$
(Linear Pair)
Dividing by 2:
$\frac{1}{2}\angle ACR + \frac{1}{2}\angle ACQ = 90^\circ$
$\angle ACD + \angle BCD = 90^\circ$
(Note: $\angle BCA = \angle BCQ$ used here, name adjusted)
$\angle BCD = 90^\circ$
The quadrilateral ABCD has all its angles equal to $90^\circ$ ($\angle ABC = 90^\circ$, $\angle BCD = 90^\circ$, $\angle CDA = 90^\circ$, $\angle DAB = 90^\circ$).
A quadrilateral with all angles equal to $90^\circ$ is a rectangle.
Hence, the quadrilateral formed by the bisectors of interior angles is a rectangle.
Example 5. Show that the bisectors of angles of a parallelogram form a rectangle.
Answer:
Given:
ABCD is a parallelogram.
AR, BR, CR, DR are the bisectors of angles $\angle A$, $\angle B$, $\angle C$, $\angle D$ respectively, forming a quadrilateral PQRS (where P is intersection of AR and DR, Q is intersection of AR and BR, R is intersection of BR and CR, S is intersection of CR and DR).
To Prove:
Quadrilateral PQRS is a rectangle.
Proof:
In parallelogram ABCD, opposite sides are parallel. So, AD $||$ BC and AB $||$ DC.
Since AD $||$ BC and AB is a transversal, the sum of consecutive interior angles is $180^\circ$.
$\angle DAB + \angle ABC = 180^\circ$
(Consecutive interior angles)
AR bisects $\angle DAB$ and BR bisects $\angle ABC$.
$\angle RAB = \frac{1}{2} \angle DAB$
$\angle RBA = \frac{1}{2} \angle ABC$
Therefore,
$\frac{1}{2} \angle DAB + \frac{1}{2} \angle ABC = \frac{1}{2} \times 180^\circ$
$\angle RAB + \angle RBA = 90^\circ$
... (1)
Consider $\triangle ARB$ (using the intersection point R from the description, though standard notation uses Q for intersection of AR and BR). Let's use standard notation PQRS where P=DR∩CR, Q=AR∩BR, R=BR∩CR, S=DR∩AR.
In $\triangle AQB$ (using standard notation):
$\angle QAB + \angle QBA + \angle AQB = 180^\circ$
(Angle sum property of triangle)
Using (1):
$90^\circ + \angle AQB = 180^\circ$
$\angle AQB = 180^\circ - 90^\circ = 90^\circ$
Since $\angle AQB$ and $\angle PQR$ are vertically opposite angles:
$\angle PQR = \angle AQB = 90^\circ$
(Vertically opposite angles)
Similarly, consider adjacent angles $\angle BCD$ and $\angle CDA$.
$\angle BCD + \angle CDA = 180^\circ$
(Consecutive interior angles)
CR bisects $\angle BCD$ and DR bisects $\angle CDA$.
$\frac{1}{2} \angle BCD + \frac{1}{2} \angle CDA = \frac{1}{2} \times 180^\circ$
$\angle RCD + \angle RDC = 90^\circ$
In $\triangle CRD$ (or $\triangle PSD$ using standard notation):
$\angle SCR + \angle SDC + \angle DSC = 180^\circ$
(Angle sum property of triangle)
$90^\circ + \angle DSC = 180^\circ$
$\angle DSC = 90^\circ$
Since $\angle DSC$ and $\angle PSR$ are vertically opposite angles:
$\angle PSR = \angle DSC = 90^\circ$
(Vertically opposite angles)
Similarly, by considering angles $\angle A$ and $\angle D$, we find $\angle ASD = 90^\circ$, which means $\angle QSP = 90^\circ$.
And by considering angles $\angle B$ and $\angle C$, we find $\angle BRC = 90^\circ$, which means $\angle QRC = 90^\circ$.
So, the quadrilateral PQRS has all its angles equal to $90^\circ$ ($\angle PQR = 90^\circ, \angle QRS = 90^\circ, \angle RSP = 90^\circ, \angle SPQ = 90^\circ$).
Therefore, PQRS is a rectangle.
Example 6. ABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that:
(i) APCQ is a parallelogram.
(ii) DPBQ is a parallelogram.
(iii) PSQR is a parallelogram.
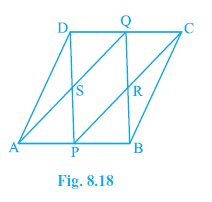
Answer:
Given:
ABCD is a parallelogram.
P is the mid-point of AB.
Q is the mid-point of CD.
AQ intersects DP at S.
BQ intersects CP at R.
To Prove:
(i) APCQ is a parallelogram.
(ii) DPBQ is a parallelogram.
(iii) PSQR is a parallelogram.
Proof:
Part (i): APCQ is a parallelogram
Since ABCD is a parallelogram:
AB $||$ DC
(Opposite sides of parallelogram)
AB = DC
(Opposite sides of parallelogram)
Since AB $||$ DC, it follows that AP $||$ QC (as AP is part of AB and QC is part of DC).
P is the mid-point of AB, so $AP = \frac{1}{2} AB$.
Q is the mid-point of DC, so $QC = \frac{1}{2} DC$.
Since AB = DC, we have $\frac{1}{2} AB = \frac{1}{2} DC$.
AP = QC
... (1)
Now, in quadrilateral APCQ, we have:
AP $||$ QC (Proved above)
AP = QC (From (1))
A quadrilateral is a parallelogram if one pair of opposite sides is equal and parallel.
Therefore, APCQ is a parallelogram.
Part (ii): DPBQ is a parallelogram
Similarly, since AB $||$ DC, it follows that PB $||$ DQ (as PB is part of AB and DQ is part of DC).
P is the mid-point of AB, so $PB = \frac{1}{2} AB$.
Q is the mid-point of DC, so $DQ = \frac{1}{2} DC$.
Since AB = DC, we have $\frac{1}{2} AB = \frac{1}{2} DC$.
PB = DQ
... (2)
Now, in quadrilateral DPBQ, we have:
PB $||$ DQ (Proved above)
PB = DQ (From (2))
A quadrilateral is a parallelogram if one pair of opposite sides is equal and parallel.
Therefore, DPBQ is a parallelogram.
Part (iii): PSQR is a parallelogram
From Part (i), APCQ is a parallelogram.
Therefore, its opposite sides are parallel.
AQ $||$ PC
Since S lies on AQ and R lies on PC, this implies:
SQ $||$ PR
From Part (ii), DPBQ is a parallelogram.
Therefore, its opposite sides are parallel.
DP $||$ QB
Since S lies on DP and R lies on QB, this implies:
SP $||$ QR
Now, in quadrilateral PSQR, we have both pairs of opposite sides parallel:
SQ $||$ PR
SP $||$ QR
A quadrilateral is a parallelogram if both pairs of opposite sides are parallel.
Therefore, PSQR is a parallelogram.
Exercise 8.1
Question 1. The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Answer:
Given:
The angles of a quadrilateral are in the ratio $3 : 5 : 9 : 13$.
To Find:
All the angles of the quadrilateral.
Solution:
Let the angles of the quadrilateral be $3x$, $5x$, $9x$, and $13x$.
The sum of the angles of a quadrilateral is $360^\circ$.
Therefore,
$3x + 5x + 9x + 13x = 360^\circ$
$30x = 360^\circ$
$x = \frac{360^\circ}{30}$
$x = 12^\circ$
Now, we find each angle:
First angle = $3x = 3 \times 12^\circ = 36^\circ$
Second angle = $5x = 5 \times 12^\circ = 60^\circ$
Third angle = $9x = 9 \times 12^\circ = 108^\circ$
Fourth angle = $13x = 13 \times 12^\circ = 156^\circ$
The angles of the quadrilateral are $36^\circ, 60^\circ, 108^\circ, 156^\circ$.
(Check: $36 + 60 + 108 + 156 = 96 + 264 = 360^\circ$. The sum is correct.)
Question 2. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Answer:
Given:
ABCD is a parallelogram.
Diagonal AC = Diagonal BD.
To Prove:
ABCD is a rectangle.
Proof:
Consider $\triangle ABC$ and $\triangle DCB$.
AB = DC
(Opposite sides of a parallelogram are equal)
BC = CB
(Common side)
AC = DB
(Given)
Therefore, by SSS (Side-Side-Side) congruence rule:
$\triangle ABC \cong \triangle DCB$
By CPCT (Corresponding Parts of Congruent Triangles):
$\angle ABC = \angle DCB$
... (i)
Since ABCD is a parallelogram, the opposite sides AB and DC are parallel (AB $||$ DC).
Considering BC as a transversal, the sum of consecutive interior angles is $180^\circ$.
$\angle ABC + \angle DCB = 180^\circ$
(Consecutive interior angles)
Using equation (i):
$\angle ABC + \angle ABC = 180^\circ$
$2 \angle ABC = 180^\circ$
$\angle ABC = \frac{180^\circ}{2}$
$\angle ABC = 90^\circ$
A parallelogram with one angle equal to $90^\circ$ is a rectangle.
Therefore, ABCD is a rectangle.
Question 3. Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Answer:
Given:
ABCD is a quadrilateral.
Diagonals AC and BD intersect at O.
AO = OC and BO = OD (Diagonals bisect each other).
AC $\perp$ BD, i.e., $\angle AOB = \angle BOC = \angle COD = \angle DOA = 90^\circ$.
To Prove:
ABCD is a rhombus.
Proof:
Since the diagonals of quadrilateral ABCD bisect each other (AO = OC and BO = OD), ABCD is a parallelogram.
Now, we need to show that the adjacent sides of the parallelogram are equal.
Consider $\triangle AOD$ and $\triangle COD$.
AO = CO
(Given)
$\angle AOD = \angle COD$
(Each $90^\circ$, Given)
OD = OD
(Common side)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle AOD \cong \triangle COD$
By CPCT (Corresponding Parts of Congruent Triangles):
AD = CD
Since ABCD is a parallelogram, opposite sides are equal:
AD = BC and AB = CD
Combining these results:
AB = CD = AD = BC
A parallelogram with all sides equal is a rhombus.
Alternatively, a parallelogram with adjacent sides equal (AD = CD) is a rhombus.
Therefore, ABCD is a rhombus.
Question 4. Show that the diagonals of a square are equal and bisect each other at right angles.
Answer:
Given:
ABCD is a square.
Diagonals AC and BD intersect at O.
To Prove:
1. Diagonals are equal (AC = BD).
2. Diagonals bisect each other (AO = OC and BO = OD).
3. Diagonals bisect each other at right angles (AC $\perp$ BD, i.e., $\angle AOB = 90^\circ$).
Proof:
Part 1: Diagonals are equal (AC = BD)
Consider $\triangle ABC$ and $\triangle BAD$.
AB = BA
(Common side)
BC = AD
(Sides of a square are equal)
$\angle ABC = \angle BAD$
(Each angle of a square is $90^\circ$)
Therefore, by SAS congruence rule:
$\triangle ABC \cong \triangle BAD$
By CPCT:
AC = BD. (Diagonals are equal)
Part 2: Diagonals bisect each other (AO = OC and BO = OD)
A square is a special type of parallelogram.
We know that the diagonals of a parallelogram bisect each other.
Therefore, for square ABCD:
AO = OC and BO = OD. (Diagonals bisect each other)
Part 3: Diagonals bisect each other at right angles (AC $\perp$ BD)
Consider $\triangle AOB$ and $\triangle COB$.
AB = CB
(Sides of a square are equal)
AO = CO
(Proved in Part 2, diagonals bisect)
OB = OB
(Common side)
Therefore, by SSS congruence rule:
$\triangle AOB \cong \triangle COB$
By CPCT:
$\angle AOB = \angle COB$
... (i)
Also, AC is a straight line, so $\angle AOB$ and $\angle COB$ form a linear pair.
$\angle AOB + \angle COB = 180^\circ$
(Linear Pair Axiom)
Using equation (i):
$\angle AOB + \angle AOB = 180^\circ$
$2 \angle AOB = 180^\circ$
$\angle AOB = 90^\circ$
Thus, the diagonals intersect at right angles.
Combining the results, the diagonals of a square are equal, bisect each other, and intersect at right angles.
Question 5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Answer:
Given:
ABCD is a quadrilateral.
Diagonals AC and BD intersect at O.
AC = BD (Diagonals are equal).
AO = OC and BO = OD (Diagonals bisect each other).
AC $\perp$ BD (Diagonals bisect at right angles, $\angle AOB = 90^\circ$).
To Prove:
ABCD is a square.
Proof:
Step 1: Show ABCD is a parallelogram.
Since the diagonals AC and BD bisect each other (AO = OC and BO = OD), the quadrilateral ABCD is a parallelogram.
Step 2: Show the parallelogram is a rhombus.
Since the diagonals of parallelogram ABCD intersect at right angles ($\angle AOB = 90^\circ$), it is a rhombus.
(Proof: Consider $\triangle AOB$ and $\triangle COB$. AO=CO, $\angle AOB=\angle COB=90^\circ$, OB=OB. By SAS, $\triangle AOB \cong \triangle COB$. By CPCT, AB=CB. A parallelogram with adjacent sides equal is a rhombus.)
So, ABCD is a rhombus, which means all sides are equal: AB = BC = CD = DA.
Step 3: Show the rhombus is a square (by showing one angle is $90^\circ$).
Consider $\triangle ABC$ and $\triangle DCB$.
AB = DC
(Opposite sides of parallelogram/rhombus)
BC = CB
(Common side)
AC = DB
(Given, diagonals are equal)
Therefore, by SSS congruence rule:
$\triangle ABC \cong \triangle DCB$
By CPCT:
$\angle ABC = \angle DCB$
... (i)
Since ABCD is a parallelogram, AB $||$ DC.
Considering BC as a transversal:
$\angle ABC + \angle DCB = 180^\circ$
(Consecutive interior angles)
Using equation (i):
$\angle ABC + \angle ABC = 180^\circ$
$2 \angle ABC = 180^\circ$
$\angle ABC = 90^\circ$
Thus, ABCD is a rhombus with one angle equal to $90^\circ$.
(Alternatively, ABCD is a parallelogram with equal diagonals, making it a rectangle. Since it's also a rhombus, it has all sides equal. A rectangle with all sides equal is a square).
Therefore, ABCD is a square.
Question 6. Diagonal AC of a parallelogram ABCD bisects ∠A (see Fig. 8.19). Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
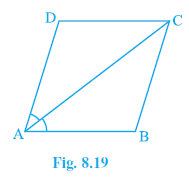
Answer:
Given:
ABCD is a parallelogram.
Diagonal AC bisects $\angle A$. This means $\angle DAC = \angle BAC$.
To Prove:
(i) AC bisects $\angle C$ (i.e., $\angle DCA = \angle BCA$).
(ii) ABCD is a rhombus.
Proof:
Part (i): AC bisects $\angle C$
Since ABCD is a parallelogram, AB $||$ DC.
Considering AC as a transversal:
$\angle BAC = \angle DCA$
[Alternate Interior Angles] ... (1)
Also, since ABCD is a parallelogram, AD $||$ BC.
Considering AC as a transversal:
$\angle DAC = \angle BCA$
[Alternate Interior Angles] ... (2)
It is given that AC bisects $\angle A$:
$\angle DAC = \angle BAC$
[Given] ... (3)
From equations (1), (2), and (3):
$\angle DAC = \angle BAC \implies \angle BCA = \angle DCA$
$\angle DCA = \angle BCA$
This means that AC bisects $\angle C$.
Hence, part (i) is proved.
Part (ii): ABCD is a rhombus
From equations (2) and (3), we have:
$\angle DAC = \angle BCA$ and $\angle DAC = \angle BAC$.
Therefore, $\angle BCA = \angle BAC$.
Now, consider $\triangle ABC$.
We have shown that $\angle BCA = \angle BAC$.
In a triangle, sides opposite to equal angles are equal.
Therefore,
AB = BC
(Sides opposite equal angles)
Since ABCD is a parallelogram, opposite sides are equal:
AB = CD and BC = DA
Combining these, we get:
AB = BC = CD = DA
A parallelogram with adjacent sides equal (or all sides equal) is a rhombus.
Therefore, ABCD is a rhombus.
Hence, part (ii) is proved.
Question 7. ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
Answer:
Given:
ABCD is a rhombus.
To Prove:
1. Diagonal AC bisects $\angle A$ and $\angle C$.
2. Diagonal BD bisects $\angle B$ and $\angle D$.
Proof:
Part 1: Diagonal AC bisects $\angle A$ and $\angle C$
Since ABCD is a rhombus, all sides are equal: AB = BC = CD = DA.
Consider $\triangle ABC$.
AB = BC
(Sides of a rhombus)
In $\triangle ABC$, angles opposite to equal sides are equal.
$\angle BAC = \angle BCA$
[Angles opp. equal sides] ... (1)
Since ABCD is a rhombus, it is also a parallelogram. So, AB $||$ DC.
Considering AC as a transversal:
$\angle BAC = \angle DCA$
[Alternate Interior Angles] ... (2)
From (1) and (2):
$\angle BCA = \angle DCA$
Therefore, AC bisects $\angle C$.
Also, since AD $||$ BC and AC is a transversal:
$\angle BCA = \angle DAC$
[Alternate Interior Angles] ... (3)
From (1) and (3):
$\angle BAC = \angle DAC$
Therefore, AC bisects $\angle A$.
Part 2: Diagonal BD bisects $\angle B$ and $\angle D$
Consider $\triangle ABD$.
AB = AD
(Sides of a rhombus)
In $\triangle ABD$, angles opposite to equal sides are equal.
$\angle ABD = \angle ADB$
[Angles opp. equal sides] ... (4)
Since AB $||$ DC and BD is a transversal:
$\angle ABD = \angle CDB$
[Alternate Interior Angles] ... (5)
From (4) and (5):
$\angle ADB = \angle CDB$
Therefore, BD bisects $\angle D$.
Also, since AD $||$ BC and BD is a transversal:
$\angle ADB = \angle CBD$
[Alternate Interior Angles] ... (6)
From (4) and (6):
$\angle ABD = \angle CBD$
Therefore, BD bisects $\angle B$.
Hence, diagonal AC bisects $\angle A$ and $\angle C$, and diagonal BD bisects $\angle B$ and $\angle D$.
Question 8. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
(i) ABCD is a square
(ii) diagonal BD bisects ∠B as well as ∠D.
Answer:
Given:
ABCD is a rectangle.
Diagonal AC bisects $\angle A$ (i.e., $\angle DAC = \angle BAC$) and $\angle C$ (i.e., $\angle DCA = \angle BCA$).
To Prove:
(i) ABCD is a square.
(ii) Diagonal BD bisects $\angle B$ and $\angle D$.
Proof:
Part (i): ABCD is a square
Since ABCD is a rectangle, all angles are $90^\circ$. So, $\angle A = \angle C = 90^\circ$.
Given that AC bisects $\angle A$:
$\angle DAC = \angle BAC = \frac{1}{2} \angle A = \frac{1}{2} \times 90^\circ = 45^\circ$.
Given that AC bisects $\angle C$:
$\angle DCA = \angle BCA = \frac{1}{2} \angle C = \frac{1}{2} \times 90^\circ = 45^\circ$.
Consider $\triangle ABC$.
We have $\angle BAC = 45^\circ$ and $\angle BCA = 45^\circ$.
Since $\angle BAC = \angle BCA$, the sides opposite to these angles are equal.
AB = BC
(Sides opposite equal angles)
ABCD is a rectangle, which is a parallelogram with one angle $90^\circ$. We have now shown that adjacent sides AB and BC are equal.
A rectangle with adjacent sides equal is a square.
Therefore, ABCD is a square.
Hence, part (i) is proved.
Part (ii): Diagonal BD bisects $\angle B$ and $\angle D$
From Part (i), we have proved that ABCD is a square.
A square is also a rhombus (since all sides are equal).
We know from the properties of a rhombus (or proved in Question 7) that the diagonals of a rhombus bisect the angles at the vertices.
Since ABCD is a square (and hence a rhombus), the diagonal BD must bisect $\angle B$ and $\angle D$.
Therefore, diagonal BD bisects $\angle B$ as well as $\angle D$.
Hence, part (ii) is proved.
Question 9. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig. 8.20). Show that:
(i) ∆ APD ≅ ∆ CQB
(ii) AP = CQ
(iii) ∆ AQB ≅ ∆ CPD
(iv) AQ = CP
(v) APCQ is a parallelogram
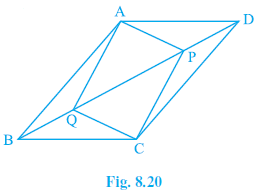
Answer:
Given:
ABCD is a parallelogram.
P and Q are points on diagonal BD such that DP = BQ.
To Prove:
(i) $\triangle APD \cong \triangle CQB$
(ii) AP = CQ
(iii) $\triangle AQB \cong \triangle CPD$
(iv) AQ = CP
(v) APCQ is a parallelogram
Proof:
Part (i): $\triangle APD \cong \triangle CQB$
Consider $\triangle APD$ and $\triangle CQB$.
AD = CB
(Opposite sides of parallelogram ABCD)
DP = BQ
(Given)
Since ABCD is a parallelogram, AD $||$ BC.
Considering BD as a transversal:
$\angle ADP = \angle CBQ$
(Alternate Interior Angles)
Therefore, by SAS congruence rule:
$\triangle APD \cong \triangle CQB$.
Part (ii): AP = CQ
Since $\triangle APD \cong \triangle CQB$ (proved in Part i),
By CPCT (Corresponding Parts of Congruent Triangles):
AP = CQ.
Part (iii): $\triangle AQB \cong \triangle CPD$
Consider $\triangle AQB$ and $\triangle CPD$.
AB = CD
(Opposite sides of parallelogram ABCD)
BQ = DP
(Given)
Since ABCD is a parallelogram, AB $||$ DC.
Considering BD as a transversal:
$\angle ABQ = \angle CDP$
(Alternate Interior Angles)
Therefore, by SAS congruence rule:
$\triangle AQB \cong \triangle CPD$.
Part (iv): AQ = CP
Since $\triangle AQB \cong \triangle CPD$ (proved in Part iii),
By CPCT:
AQ = CP.
Part (v): APCQ is a parallelogram
Consider the quadrilateral APCQ.
From Part (ii), we have AP = CQ.
From Part (iv), we have AQ = CP.
Since both pairs of opposite sides of quadrilateral APCQ are equal, APCQ is a parallelogram.
Therefore, APCQ is a parallelogram.
Question 10. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.21). Show that
(i) ∆ APB ≅ ∆ CQD
(ii) AP = CQ
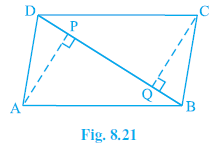
Answer:
Given:
ABCD is a parallelogram.
AP $\perp$ BD and CQ $\perp$ BD.
To Prove:
(i) $\triangle APB \cong \triangle CQD$
(ii) AP = CQ
Proof:
Part (i): $\triangle APB \cong \triangle CQD$
Consider $\triangle APB$ and $\triangle CQD$.
$\angle APB = 90^\circ$
(Given AP $\perp$ BD)
$\angle CQD = 90^\circ$
(Given CQ $\perp$ BD)
So, $\angle APB = \angle CQD$.
AB = CD
(Opposite sides of parallelogram ABCD)
Since ABCD is a parallelogram, AB $||$ DC.
Considering BD as a transversal:
$\angle ABP = \angle CDQ$
(Alternate Interior Angles)
Therefore, by AAS (Angle-Angle-Side) congruence rule:
$\triangle APB \cong \triangle CQD$.
Part (ii): AP = CQ
Since $\triangle APB \cong \triangle CQD$ (proved in Part i),
By CPCT (Corresponding Parts of Congruent Triangles):
AP = CQ.
Question 11. In ∆ ABC and ∆ DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig. 8.22). Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ ABC ≅ ∆ DEF.
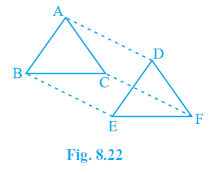
Answer:
Given:
In $\triangle ABC$ and $\triangle DEF$:
AB = DE and AB $||$ DE.
BC = EF and BC $||$ EF.
Vertices A, B, C are joined to vertices D, E, F respectively.
To Prove:
(i) Quadrilateral ABED is a parallelogram.
(ii) Quadrilateral BEFC is a parallelogram.
(iii) AD $||$ CF and AD = CF.
(iv) Quadrilateral ACFD is a parallelogram.
(v) AC = DF.
(vi) $\triangle ABC \cong \triangle DEF$.
Proof:
Part (i): Quadrilateral ABED is a parallelogram
Consider quadrilateral ABED.
We are given that AB = DE and AB $||$ DE.
A quadrilateral is a parallelogram if one pair of opposite sides is equal and parallel.
Therefore, quadrilateral ABED is a parallelogram.
Part (ii): Quadrilateral BEFC is a parallelogram
Consider quadrilateral BEFC.
We are given that BC = EF and BC $||$ EF.
A quadrilateral is a parallelogram if one pair of opposite sides is equal and parallel.
Therefore, quadrilateral BEFC is a parallelogram.
Part (iii): AD $||$ CF and AD = CF
From Part (i), ABED is a parallelogram.
Opposite sides of a parallelogram are equal and parallel.
AD = BE and AD $||$ BE
[Opp. sides of $||$gm ABED] ... (1)
From Part (ii), BEFC is a parallelogram.
Opposite sides of a parallelogram are equal and parallel.
CF = BE and CF $||$ BE
[Opp. sides of $||$gm BEFC] ... (2)
From (1) and (2):
AD = BE and CF = BE $\implies$ AD = CF.
AD $||$ BE and CF $||$ BE $\implies$ AD $||$ CF (Lines parallel to the same line are parallel to each other).
Part (iv): Quadrilateral ACFD is a parallelogram
Consider quadrilateral ACFD.
From Part (iii), we have proved that AD = CF and AD $||$ CF.
A quadrilateral is a parallelogram if one pair of opposite sides is equal and parallel.
Therefore, quadrilateral ACFD is a parallelogram.
Part (v): AC = DF
Since ACFD is a parallelogram (proved in Part iv), its opposite sides are equal.
Therefore, AC = DF.
Part (vi): $\triangle ABC \cong \triangle DEF$
Consider $\triangle ABC$ and $\triangle DEF$.
AB = DE
(Given)
BC = EF
(Given)
AC = DF
(Proved in Part v)
Therefore, by SSS congruence rule:
$\triangle ABC \cong \triangle DEF$.
Question 12. ABCD is a trapezium in which AB || CD and AD = BC (see Fig. 8.23). Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ ABC ≅ ∆ BAD
(iv) diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
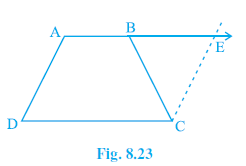
Answer:
Given:
ABCD is a trapezium.
AB $||$ CD.
AD = BC.
Construction:
Extend AB to E.
Draw a line through C parallel to DA (CE $||$ DA), intersecting the extended line AE at E.
To Prove:
(i) $\angle A = \angle B$
(ii) $\angle C = \angle D$
(iii) $\triangle ABC \cong \triangle BAD$
(iv) Diagonal AC = Diagonal BD
Proof:
Part (i): $\angle A = \angle B$
By construction, AE $||$ DC (since AB $||$ DC and AE is extension of AB).
Also by construction, AD $||$ CE.
Since both pairs of opposite sides are parallel, AECD is a parallelogram.
Opposite sides of a parallelogram are equal:
AD = CE
... (1)
It is given that:
AD = BC
... (2)
From (1) and (2):
BC = CE
Now consider $\triangle BCE$.
Since BC = CE, angles opposite to equal sides are equal:
$\angle CBE = \angle CEB$
[Angles opp. equal sides] ... (3)
Since AD $||$ CE (by construction) and AE is a transversal:
$\angle DAB + \angle CEB = 180^\circ$
(Consecutive Interior Angles)
Also, ABE is a straight line, so $\angle ABC$ and $\angle CBE$ form a linear pair:
$\angle ABC + \angle CBE = 180^\circ$
(Linear Pair)
So, $\angle DAB + \angle CEB = \angle ABC + \angle CBE = 180^\circ$.
This implies $\angle DAB + \angle CEB = \angle ABC + \angle CBE$.
Using $\angle CBE = \angle CEB$ from (3):
$\angle DAB + \angle CEB = \angle ABC + \angle CEB$
$\angle DAB = \angle ABC$
Therefore, $\angle A = \angle B$.
Part (ii): $\angle C = \angle D$
Since AB $||$ CD, and AD and BC are transversals.
Sum of consecutive interior angles are supplementary:
$\angle A + \angle D = 180^\circ$
... (4)
$\angle B + \angle C = 180^\circ$
... (5)
From (4) and (5):
$\angle A + \angle D = \angle B + \angle C$
Since we proved $\angle A = \angle B$ in Part (i):
$\angle B + \angle D = \angle B + \angle C$
$\angle D = \angle C$
Therefore, $\angle C = \angle D$.
Part (iii): $\triangle ABC \cong \triangle BAD$
Consider $\triangle ABC$ and $\triangle BAD$.
AB = BA
(Common side)
BC = AD
(Given)
$\angle ABC = \angle BAD$
(Proved in Part i)
Therefore, by SAS congruence rule:
$\triangle ABC \cong \triangle BAD$.
Part (iv): Diagonal AC = Diagonal BD
Since $\triangle ABC \cong \triangle BAD$ (proved in Part iii),
By CPCT:
AC = BD.
Thus, the diagonals are equal.
Example 7 & 8 (Before Exercise 8.2)
Example 7. In ∆ ABC, D, E and F are respectively the mid-points of sides AB, BC and CA (see Fig. 8.27). Show that ∆ ABC is divided into four congruent triangles by joining D, E and F.

Answer:
Given:
In $\triangle ABC$, D, E, and F are the mid-points of sides AB, BC, and CA respectively.
To Prove:
Joining D, E, and F divides $\triangle ABC$ into four congruent triangles: $\triangle ADF \cong \triangle BDE \cong \triangle CFE \cong \triangle DEF$.
Proof:
Since D and E are the mid-points of sides AB and BC of $\triangle ABC$, by the Mid-point Theorem:
DE $||$ AC and $DE = \frac{1}{2} AC$
Since F is the mid-point of AC, $AF = FC = \frac{1}{2} AC$.
Therefore, DE $||$ FC and DE = FC.
Also, DE $||$ AF and DE = AF.
Similarly, since E and F are the mid-points of BC and CA:
EF $||$ AB and $EF = \frac{1}{2} AB$. Since D is the mid-point of AB, $AD = DB = \frac{1}{2} AB$.
Therefore, EF $||$ DB and EF = DB.
Also, EF $||$ AD and EF = AD.
And, since D and F are the mid-points of AB and CA:
DF $||$ BC and $DF = \frac{1}{2} BC$. Since E is the mid-point of BC, $BE = EC = \frac{1}{2} BC$.
Therefore, DF $||$ EC and DF = EC.
Also, DF $||$ BE and DF = BE.
Now consider quadrilateral ADFE.
We have AD $||$ EF and AF $||$ DE.
So, ADFE is a parallelogram (both pairs of opposite sides are parallel).
The diagonal DF divides the parallelogram ADFE into two congruent triangles.
$\triangle ADF \cong \triangle DEF$ ... (i)
Consider quadrilateral BDFE.
We have BD $||$ EF and BE $||$ DF.
So, BDFE is a parallelogram.
The diagonal DE divides the parallelogram BDFE into two congruent triangles.
$\triangle BDE \cong \triangle DEF$ ... (ii)
Consider quadrilateral CFDE.
We have CF $||$ DE and CE $||$ DF.
So, CFDE is a parallelogram.
The diagonal EF divides the parallelogram CFDE into two congruent triangles.
$\triangle CFE \cong \triangle DEF$ ... (iii)
From (i), (ii), and (iii), we can conclude that:
$\triangle ADF \cong \triangle BDE \cong \triangle CFE \cong \triangle DEF$.
Thus, joining the mid-points D, E, and F divides $\triangle ABC$ into four congruent triangles.
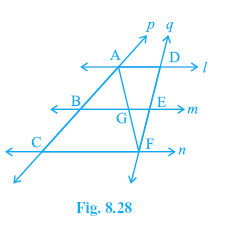
Example 8. l, m and n are three parallel lines intersected by transversals p and q such that l, m and n cut off equal intercepts AB and BC on p (see Fig. 8.28). Show that l, m and n cut off equal intercepts DE and EF on q also.
Answer:
Given:
Three parallel lines $l$, $m$, $n$. ($l \parallel m \parallel n$).
Transversals $p$ and $q$ intersect $l, m, n$ at A, B, C and D, E, F respectively.
The intercepts on $p$ are equal: AB = BC.
To Prove:
The intercepts on $q$ are equal: DE = EF.
Construction:
Join A to F, intersecting the line $m$ at point G.
Proof:
Consider $\triangle ACF$.
B is the mid-point of AC
(Since AB = BC is given)
Line $m$ is parallel to line $n$ ($m \parallel n$).
So, BG $||$ CF (since BG is part of line $m$ and CF is part of line $n$).
By the Converse of the Mid-point Theorem applied to $\triangle ACF$:
A line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.
Therefore, G must be the mid-point of AF.
AG = GF
... (i)
Now consider $\triangle AFD$.
G is the mid-point of AF
(Proved above in (i))
Line $l$ is parallel to line $m$ ($l \parallel m$).
So, AD $||$ GE (since AD is part of line $l$ and GE is part of line $m$).
By the Converse of the Mid-point Theorem applied to $\triangle AFD$:
A line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.
Therefore, E must be the mid-point of DF.
DE = EF
Hence, the lines $l, m, n$ cut off equal intercepts DE and EF on transversal $q$.
Exercise 8.2
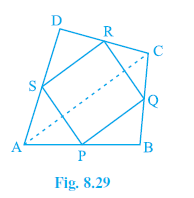
Question 1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.29). AC is a diagonal. Show that :
(i) SR || AC and SR = $\frac{1}{2}$ AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Answer:
Given:
A quadrilateral ABCD.
P, Q, R, S are the mid-points of sides AB, BC, CD, DA respectively.
AC is a diagonal.
To Prove:
(i) SR $||$ AC and SR = $\frac{1}{2}$ AC
(ii) PQ = SR
(iii) PQRS is a parallelogram
Proof:
Part (i): SR $||$ AC and SR = $\frac{1}{2}$ AC
Consider $\triangle ADC$.
S is the mid-point of side DA (Given).
R is the mid-point of side DC (Given).
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of it.
Therefore, in $\triangle ADC$:
SR $||$ AC
and SR = $\frac{1}{2}$ AC ... (1)
Part (ii): PQ = SR
Consider $\triangle ABC$.
P is the mid-point of side AB (Given).
Q is the mid-point of side BC (Given).
By the Mid-point Theorem, in $\triangle ABC$:
PQ $||$ AC
and PQ = $\frac{1}{2}$ AC ... (2)
From equation (1), we have SR = $\frac{1}{2}$ AC.
From equation (2), we have PQ = $\frac{1}{2}$ AC.
Comparing these, we get:
PQ = SR.
Part (iii): PQRS is a parallelogram
From the proofs in Part (i) and Part (ii):
SR $||$ AC (from (1))
PQ $||$ AC (from (2))
Since PQ and SR are both parallel to the same line AC, they must be parallel to each other.
PQ $||$ SR
Also, from Part (ii), we have:
PQ = SR
Now consider the quadrilateral PQRS.
We have shown that one pair of opposite sides (PQ and SR) is both equal and parallel.
A quadrilateral is a parallelogram if one pair of opposite sides is equal and parallel.
Therefore, PQRS is a parallelogram.
Question 2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Answer:
Given:
ABCD is a rhombus.
P, Q, R, and S are the mid-points of the sides AB, BC, CD, and DA respectively.
To Prove:
The quadrilateral PQRS is a rectangle.
Construction:
Join the diagonals AC and BD of the rhombus ABCD.
Proof:
First, we will prove that PQRS is a parallelogram.
In $\triangle ABC$:
P is the mid-point of AB (Given).
Q is the mid-point of BC (Given).
By the Mid-point Theorem, which states that the line segment joining the mid-points of two sides of a triangle is parallel to the third side and half of it, we have:
$PQ || AC \text{ and } PQ = \frac{1}{2} AC$
... (i)
Now, in $\triangle ADC$:
S is the mid-point of DA (Given).
R is the mid-point of CD (Given).
By the Mid-point Theorem:
$SR || AC \text{ and } SR = \frac{1}{2} AC$
... (ii)
From equations (i) and (ii), we can conclude that:
$PQ || SR$ and $PQ = SR$
Since one pair of opposite sides of the quadrilateral PQRS is equal and parallel, PQRS is a parallelogram.
Now, we will prove that one of the interior angles of the parallelogram PQRS is a right angle.
In $\triangle ABD$:
P is the mid-point of AB (Given).
S is the mid-point of DA (Given).
By the Mid-point Theorem:
$PS || BD$
... (iii)
We know that the diagonals of a rhombus are perpendicular to each other.
Therefore, $AC \perp BD$.
Let the diagonals intersect at point O. Let PQ intersect BD at M and PS intersect AC at N.
Consider the quadrilateral MONP.
From (i), $PQ || AC \implies PM || ON$.
From (iii), $PS || BD \implies PN || OM$.
Since both pairs of opposite sides are parallel, MONP is a parallelogram.
As $AC \perp BD$, we have $\angle MON = 90^\circ$.
In a parallelogram, opposite angles are equal. Therefore:
$\angle MPN = \angle MON = 90^\circ$
Since $\angle MPN$ is the same as $\angle QPS$, we have:
$\angle QPS = 90^\circ$
We have proved that PQRS is a parallelogram with one angle equal to $90^\circ$.
A parallelogram with one right angle is a rectangle.
Therefore, the quadrilateral PQRS is a rectangle.
Hence, proved.
Question 3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Answer:
Given:
ABCD is a rectangle.
P, Q, R, and S are the mid-points of the sides AB, BC, CD, and DA respectively.
To Prove:
The quadrilateral PQRS is a rhombus.
Construction:
Join the diagonals AC and BD of the rectangle ABCD.
Proof:
First, we will prove that PQRS is a parallelogram.
In $\triangle ABC$:
P is the mid-point of AB and Q is the mid-point of BC (Given).
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and half of it. Therefore,
$PQ || AC \text{ and } PQ = \frac{1}{2} AC$
... (i)
Now, in $\triangle ADC$:
S is the mid-point of DA and R is the mid-point of CD (Given).
By the Mid-point Theorem:
$SR || AC \text{ and } SR = \frac{1}{2} AC$
... (ii)
From equations (i) and (ii), we get:
$PQ || SR$ and $PQ = SR$
Since one pair of opposite sides of the quadrilateral PQRS is equal and parallel, PQRS is a parallelogram.
Now, we need to prove that the adjacent sides of this parallelogram are equal.
In $\triangle ABD$:
P is the mid-point of AB and S is the mid-point of DA (Given).
By the Mid-point Theorem:
$PS || BD \text{ and } PS = \frac{1}{2} BD$
... (iii)
We know that the diagonals of a rectangle are equal in length.
AC = BD
(Diagonals of a rectangle are equal)
Multiplying both sides by $\frac{1}{2}$:
$\frac{1}{2} AC = \frac{1}{2} BD$
From equations (i) and (iii), we can substitute the values:
$PQ = PS$
We have shown that PQRS is a parallelogram in which a pair of adjacent sides (PQ and PS) are equal.
A parallelogram with adjacent sides equal is a rhombus.
Therefore, the quadrilateral PQRS is a rhombus.
Hence, proved.
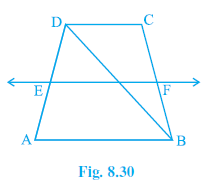
Question 4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
Answer:
Given:
ABCD is a trapezium with AB $||$ DC.
E is the mid-point of AD.
A line through E is parallel to AB (EF $||$ AB) and intersects BC at F.
BD is a diagonal.
To Prove:
F is the mid-point of BC.
Construction:
Let the line EF intersect the diagonal BD at point G.
Proof:
Consider $\triangle DAB$.
E is the mid-point of AD
(Given)
We are given EF $||$ AB.
Therefore, EG $||$ AB (since EG is part of the line EF).
By the Converse of the Mid-point Theorem (a line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side):
In $\triangle DAB$, the line EG passes through the mid-point E of AD and is parallel to side AB. Therefore, it must bisect the third side DB.
So, G is the mid-point of DB.
Now, consider $\triangle BCD$.
G is the mid-point of DB
(Proved above)
We are given AB $||$ DC and EF $||$ AB.
Since lines parallel to the same line are parallel to each other, we have EF $||$ DC.
Therefore, GF $||$ DC (since GF is part of the line EF).
By the Converse of the Mid-point Theorem applied to $\triangle BCD$:
In $\triangle BCD$, the line GF passes through the mid-point G of DB and is parallel to side DC. Therefore, it must bisect the third side BC.
So, F is the mid-point of BC.
Hence, F is the mid-point of BC.
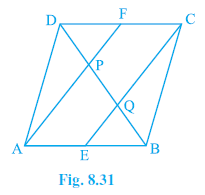
Question 5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig. 8.31). Show that the line segments AF and EC trisect the diagonal BD.
Answer:
Given:
ABCD is a parallelogram.
E is the mid-point of AB.
F is the mid-point of CD.
Line segments AF and EC intersect the diagonal BD at points P and Q respectively.
To Prove:
AF and EC trisect BD (i.e., DP = PQ = QB).
Proof:
First, we show that AECF is a parallelogram.
Since ABCD is a parallelogram:
AB $||$ DC
(Opposite sides of $||$gm)
AB = DC
(Opposite sides of $||$gm)
Since AB $||$ DC, it follows that AE $||$ FC (as AE is part of AB and FC is part of DC).
E is the mid-point of AB $\implies AE = \frac{1}{2} AB$.
F is the mid-point of DC $\implies FC = \frac{1}{2} DC$.
Since AB = DC, $\frac{1}{2} AB = \frac{1}{2} DC$, which means $AE = FC$.
Now, in quadrilateral AECF, we have AE $||$ FC and AE = FC.
Since one pair of opposite sides is equal and parallel, AECF is a parallelogram.
Therefore, the opposite sides AF and EC are parallel:
AF $||$ EC ... (1)
This implies AP $||$ EQ and PF $||$ QC.
Now, consider $\triangle DCQ$.
F is the mid-point of DC
(Given)
From (1), we know AF $||$ EC, which means PF $||$ QC.
By the Converse of the Mid-point Theorem applied to $\triangle DCQ$:
The line PF passes through the mid-point F of DC and is parallel to side QC. Therefore, it must bisect the third side DQ.
So, P is the mid-point of DQ.
DP = PQ
... (2)
Next, consider $\triangle ABP$.
E is the mid-point of AB
(Given)
From (1), we know AF $||$ EC, which means AP $||$ EQ.
By the Converse of the Mid-point Theorem applied to $\triangle ABP$:
The line EQ passes through the mid-point E of AB and is parallel to side AP. Therefore, it must bisect the third side PB.
So, Q is the mid-point of PB.
PQ = QB
... (3)
From equations (2) and (3):
DP = PQ and PQ = QB
Therefore, DP = PQ = QB.
This shows that the points P and Q divide the diagonal BD into three equal parts.
Hence, the line segments AF and EC trisect the diagonal BD.
Question 6. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Answer:
Given:
A quadrilateral ABCD.
P, Q, R, S are the mid-points of sides AB, BC, CD, DA respectively.
The line segments joining the mid-points of opposite sides are PR and QS.
To Prove:
PR and QS bisect each other.
Construction:
Join P, Q, R, S in order. Join the diagonal AC.
Proof:
Consider $\triangle ADC$.
S is the mid-point of DA and R is the mid-point of DC.
By Mid-point Theorem: SR $||$ AC and SR = $\frac{1}{2}$ AC ... (1)
Consider $\triangle ABC$.
P is the mid-point of AB and Q is the mid-point of BC.
By Mid-point Theorem: PQ $||$ AC and PQ = $\frac{1}{2}$ AC ... (2)
From (1) and (2):
PQ $||$ SR and PQ = SR.
Now consider the quadrilateral PQRS.
Since one pair of opposite sides (PQ and SR) is equal and parallel, PQRS is a parallelogram.
We know that the diagonals of a parallelogram bisect each other.
The line segments PR and QS are the diagonals of the parallelogram PQRS.
Therefore, PR and QS must bisect each other.
Hence, the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Question 7. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = $\frac{1}{2}$ AB
Answer:
Given:
$\triangle ABC$ is right-angled at C ($\angle C = 90^\circ$).
M is the mid-point of hypotenuse AB.
A line through M is parallel to BC (MD $||$ BC) and intersects AC at D.
To Prove:
(i) D is the mid-point of AC.
(ii) MD $\perp$ AC.
(iii) CM = MA = $\frac{1}{2}$ AB.
Proof:
Part (i): D is the mid-point of AC
Consider $\triangle ABC$.
M is the mid-point of AB
(Given)
MD $||$ BC
(Given)
By the Converse of the Mid-point Theorem (a line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side):
The line MD passes through the mid-point M of AB and is parallel to side BC. Therefore, it must bisect the third side AC.
So, D is the mid-point of AC.
Part (ii): MD $\perp$ AC
We are given MD $||$ BC.
Consider AC as a transversal intersecting the parallel lines MD and BC.
The corresponding angles are equal:
$\angle ADM = \angle ACB$
(Corresponding Angles)
We are given that $\triangle ABC$ is right-angled at C.
$\angle ACB = 90^\circ$
(Given)
Therefore, $\angle ADM = 90^\circ$.
Since $\angle ADM = 90^\circ$, the line segment MD is perpendicular to AC.
So, MD $\perp$ AC.
Part (iii): CM = MA = $\frac{1}{2}$ AB
Join CM.
Consider $\triangle ADM$ and $\triangle CDM$.
AD = CD
(D is mid-point of AC, proved in (i))
$\angle ADM = \angle CDM$
(Each $90^\circ$, since MD $\perp$ AC, proved in (ii))
MD = MD
(Common side)
Therefore, by SAS (Side-Angle-Side) congruence rule:
$\triangle ADM \cong \triangle CDM$
By CPCT (Corresponding Parts of Congruent Triangles):
MA = MC
... (1)
We are given that M is the mid-point of the hypotenuse AB.
Therefore, MA = $\frac{1}{2}$ AB. ... (2)
From (1) and (2):
MC = MA = $\frac{1}{2}$ AB.
Hence, CM = MA = $\frac{1}{2}$ AB.

